完全協和音程とは
完全1度と完全4度、完全5度、完全8度の4つです。
さらに完全1度と完全8度は絶対協和音程と呼ばれることもあり、前回の記事で解説しています。
この記事では完全4度と完全5度に絞って解説していきます。

度数の数え方
度数は音程間の幹音の種類がいくつあるか数を数えていきます。
まず、最も重要なポイントは音程には0(ゼロ)が存在しないという点です。同じ高さ2つの音でも幹音は1種類ですので、1度ということができます。
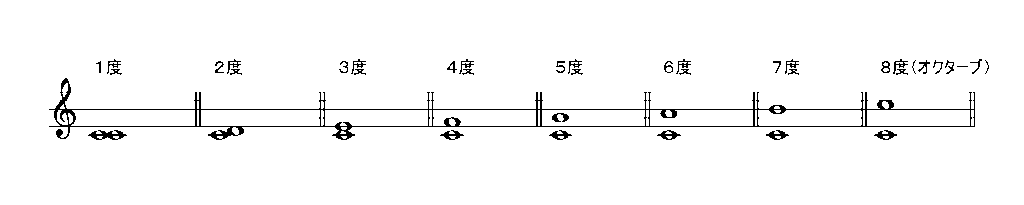
度数だけでは不完全?
例えば、ドとレ、ミとファ、これらはどちらも2度といえますよね。しかし、半音の数を数えてみると前者が半音2個分、後者が半音1個分の距離です。このように距離を表すには度数だけでは不完全なのです。
そこで、前者を長2度、後者を短2度と呼び分ける必要がでてきます。これら度数の前に付ける言葉を音程の種類と呼び、種類と度数のセットで答えることで正確になります。
次回、種類の判断方法について詳しく解説しますので、合わせてお読みください。
幹音の種類を求める
度数だけでは不十分なので、種類を合わせて呼びます。種類は「長・短・完全・増・減・重減・重増」の7種類です。
- 度数を求める
- 音程間の幹音の半音数を数える
- 表を使い、度数と半音数が交差する種類を求める
| 半音数 \ 度数 | 1 | 2、3 | 4、5 | 6、7 | 8 |
|---|---|---|---|---|---|
| 0 | 完全 | 長 | 増(ファシ) | | |
| 1 | | 短 | 完全 | 長 | |
| 2 | | | 減(シファ) | 短 | 完全 |
この表から4度と5度の幹音同士の音程は「完全」「増」「減」の3種類が付くことが分かります。
幹音同士の音程全て
全てのパターンを見てみましょう。
幹音同士の1度は「ドとファ、レとソ、ミとラ、ファとシ、ソとド、ラとレ、シとミ」の7種類しかありません。
そして基本「完全」という種類が付きます。
ファとシの音程のみ増4度となります。

幹音同士の8度も「ドとソ、レとラ、ミとシ、ファとド、ソとレ、ラとミ、シとファ」の7種類しかありません。
そして基本「完全」という種類が付きます。
シとファのみ減5度となります。

このように4度と5度の幹音同士の音程は基本「完全」という種類が付きます。
そして、「シ」と「ファ」の音の組み合わせは不協和音になってしまいます。
補足:このことから、理論が確立する前からシの音は不協和音を生みやすいとされ、しばしば♭して演奏されていました。この低いシは「丸いB」と呼ばれ、♭(フラット)の起源となります。


コメント